Designing Data Structures for Collaborative Apps

Matthew Weidner | Feb 10th, 2022
Home | RSS Feed
Keywords: collaborative apps, CRDTs, composition

I’ve put many of the ideas from this post into practice in a library, Collabs. You can learn more about Collabs, and see how open-source collaborative apps might work in practice, in my Local-First Web talk: Video, Slides, Live demo.


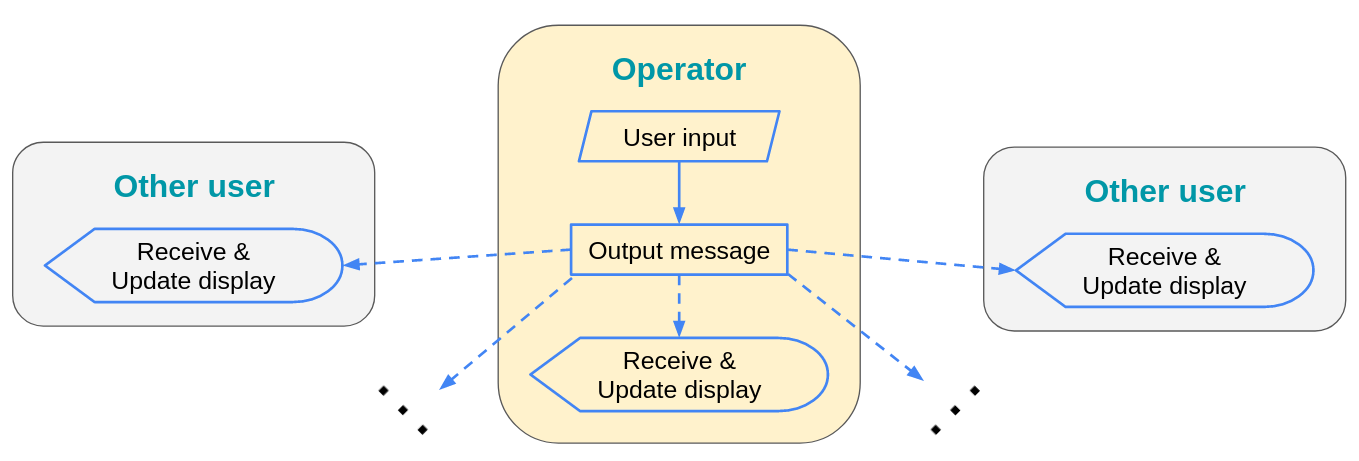
Suppose you’re building a collaborative app, along the lines of Google Docs/Sheets/Slides, Figma, Notion, etc. One challenge you’ll face is the actual collaboration: when one user changes the shared state, their changes need to show up for every other user. For example, if multiple users type at the same time in a text field, the result should reflect all of their changes and be consistent (identical for all users).

Conflict-free Replicated Data Types (CRDTs) provide a solution to this challenge. They are data structures that look like ordinary data structures (maps, sets, text strings, etc.), except that they are collaborative: when one user updates their copy of a CRDT, their changes automatically show up for everyone else. Each user sees their own changes immediately, while under the hood, the CRDT broadcasts a message describing the change to everyone else. Other users see the change once they receive this message.

CRDTs broadcast messages to relay changes

Note that multiple users might make changes at the same time, e.g., both typing at once. Since each user sees their own changes immediately, their views of the document will temporarily diverge. However, CRDTs guarantee that once the users receive each others’ messages, they’ll see identical document states again: this is the definition of CRDT correctness. Ideally, this state will also be “reasonable”, i.e., it will incorporate both of their edits in the way that the users expect.

In distributed systems terms, CRDTs are Available, Partition tolerant, and have Strong Eventual Consistency.


CRDTs work even if messages might be arbitrarily delayed, or delivered to different users in different orders. This lets you make collaborative experiences that don’t need a central server, work offline, and/or are end-to-end encrypted (local-first software).

Google Docs doesn't let you type while offline

CRDTs allow offline editing, unlike Google Docs.

I’m particularly excited by the potential for open-source collaborative apps that anyone can distribute or modify, without requiring app-specific hosting.

The Challenge: Designing CRDTs

Having read all that, let’s say you choose to use a CRDT for your collaborative app. All you need is a CRDT representing your app’s state, a frontend UI, and a network of your choice (or a way for users to pick the network themselves). But where do you get a CRDT for your specific app?

If you’re lucky, it’s described in a paper, or even better, implemented in a library. But those tend to have simple or one-size-fits-all data structures: maps, text strings, JSON, etc. You can usually rearrange your app’s state to make it fit in these CRDTs; and if users make changes at the same time, CRDT correctness guarantees that you’ll get some consistent result. However, it might not be what you or your users expect. Worse, you have little leeway to customize this behavior.

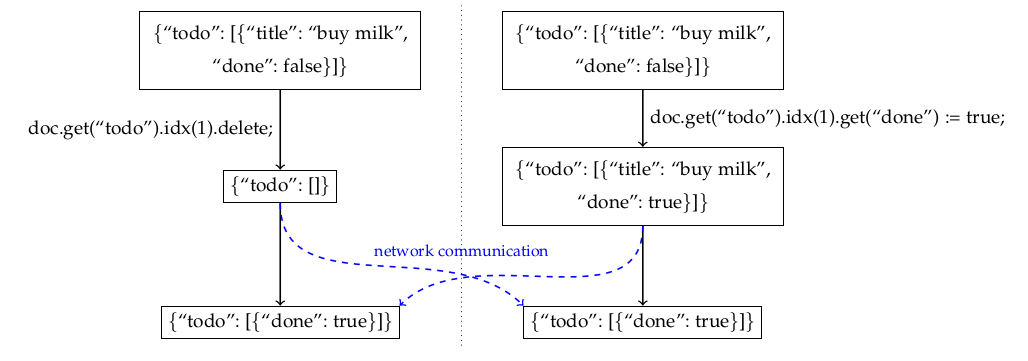
Anomaly in many map CRDTs: In a collaborative todo-list, concurrently deleting an item and marking it done results in a nonsense list item with no text field.

In many map CRDTs, when representing a todo-list using items with "title" and "done" fields, you can end up with an item {"done": true} having no "title" field. Image credit: Figure 6 by Kleppmann and Beresford.

Simulated user complaint: In a collaborative spreadsheet, concurrently moving a column and entering data might delete the entered data. If you don't control the CRDT implementation, then you can't fix this.

If a user asks you to change some behavior that comes from a CRDT library, but you don't understand the library inside and out, then it will be a hard fix.

This blog post will instead teach you how to design CRDTs from the ground up. I’ll present a few simple CRDTs that are obviously correct, plus ways to compose them together into complicated whole-app CRDTs that are still obviously correct. I’ll also present principles of CRDT design to help guide you through the process. To cap it off, we’ll design a CRDT for a collaborative spreadsheet.

Ultimately, I hope that you will gain not just an understanding of some existing CRDT designs, but also the confidence to tweak them and create your own!

Basic Designs

I’ll start by going over some basic CRDT designs.

Unique Set CRDT

Our foundational CRDT is the Unique Set. It is a set in which each added element is considered unique.

Formally, the user-facing operations on the set, and their collaborative implementations, are as follows:

In response to user input, the operator calls "Output message". The message is then delivered to every user's "Receive & Update display" function.

The lifecycle of an add or delete operation.

When displaying the set to the user, you ignore the tags and just list out the data values x, keeping in mind that (1) they are not ordered (at least not consistently across different users), and (2) there may be duplicates.

Example: In a collaborative flash card app, you could represent the deck of cards as a Unique Set, using x to hold the flash card’s value (e.g., its front and back strings). Users can edit the deck by adding a new card or deleting an existing one, and duplicate cards are allowed.

When broadcasting messages, we require that they are delivered reliably and in causal order, but it’s okay if they are arbitarily delayed. (These rules apply to all CRDTs, not just the Unique Set.) Delivery in causal order means that if a user sends a message m after receiving or sending a message m’, then all users delay receiving m until after receiving m’. This is the strictest ordering we can implement without a central server and without extra round-trips between users, e.g., by using vector clocks.

Messages that aren’t ordered by the causal order are concurrent, and different users might receive them in different orders. But for CRDT correctness, we must ensure that all users end up in the same state regardless, once they have received the same messages.

For the Unique Set, it is obvious that the state of the set, as seen by a specific user, is always the set of elements for which they have received an add message but no delete messages. This holds regardless of the order in which they received concurrent messages. Thus the Unique Set is correct.

Note that delivery in causal order is important—a delete operation only works if it is received after its corresponding add operation.


We now have our first principle of CRDT design:

Principle 1. Use the Unique Set CRDT for operations that “add” or “create” a unique new thing.

Although it is simple, the Unique Set forms the basis for the rest of our CRDTs.

Aside. Traditionally, one proves CRDT correctness by proving that concurrent messages commute—they have the same effect regardless of delivery order (Shapiro et al. 2011)—or that the final state is a function of the causally-ordered message history (Baquero, Almeida, and Shoker 2014). However, as long as you stick to the techniques in this blog post, you won’t need explicit proofs: everything builds on the Unique Set in ways that trivially preserve CRDT correctness. For example, a deterministic view of a Unique Set (or any CRDT) is obviously still a CRDT.


Aside. I have described the Unique Set in terms of operations and broadcast messages, i.e., as an operation-based CRDT. However, with some extra metadata, it is also possible to implement a merge function for the Unique Set, in the style of a state-based CRDT. Or, you can perform VCS-style 3-way merges without needing extra metadata.


List CRDT

Our next CRDT is a List CRDT. It represents a list of elements, with insert and delete operations. For example, you can use a List CRDT of characters to store the text in a collaborative text editor, using insert to type a new character and delete for backspace.

Formally, the operations on a List CRDT are:

We now need to decide on the semantics, i.e., what is the result of various insert and delete operations, possibly concurrent. The fact that insertions are unique suggests using a Unique Set (Principle 1). However, we also have to account for indices and the list order.

One approach would use indices directly: when a user calls insert(i, x), they send (i, x) to the other users, who use i to insert x at the appropriate location. The challenge is that your intended insertion index might move around as a result of users’ inserting/deleting in front of i.

The *gray* cat jumped on **the** table.

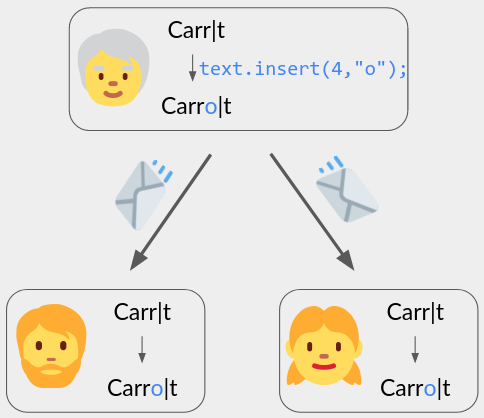
Alice typed " the" at index 17, but concurrently, Bob typed " gray" in front of her. From Bob's perspective, Alice's insert should happen at index 22.

It’s possible to work around this by “transforming” i to account for concurrent edits. That idea leads to Operational Transformation (OT), the earliest-invented approach to collaborative text editing, and the one used in Google Docs and most existing apps. Unfortunately, OT algorithms are quite complicated, leading to numerous flawed algorithms. You can reduce complexity by using a central server to manage the document, like Google Docs does, but that precludes decentralized networks, end-to-end encryption, and server-optional open-source apps.

List CRDTs use a different perspective from OT. When you type a character in a text document, you probably don’t think of its position as “index 17” or whatever; instead, its position is at a certain place within the existing text.

“A certain place within the existing text” is vague, but at a minimum, it should be between the characters left and right of your insertion point (“on” and “ table” in the example above) Also, unlike an index, this intuitive position doesn’t change if other users concurrently type earlier in the document; your new text should go between the same characters as before. That is, the position is immutable.

This leads to the following implementation. The list’s state is a Unique Set whose values are pairs (p, x), where x is the actual value (e.g., a character), and p is a unique immutable position drawn from some abstract total order. The user-visible state of the list is the list of values x ordered by their positions p. Operations are implemented as:

Of course, we need a way to create the positions p. That’s the hard part—in fact, the hardest part of any CRDT—and I don’t have space to go into it here; you should use an existing algorithm (e.g., RGA) or implementation (e.g., Yjs’s Y.Array). Update: I’ve since published two libraries for creating and using CRDT-style positions in TypeScript: list-positions (most efficient), position-strings (most flexible). Both use the Fugue algorithm.

The important lesson here is that we had to translate indices (the language of normal, non-CRDT lists) into unique immutable positions (what the user intuitively means when they say “insert here”). That leads to our second principle of CRDT design:

Principle 2. Express operations in terms of user intention—what the operation means to the user, intuitively. This might differ from the closest ordinary data type operation.

This principle works because users often have some idea what one operation should do in the face of concurrent operations. If you can capture that intuition, then the resulting operations won’t conflict.

Registers

Our last basic CRDT is the Register. This is a variable that holds an arbitrary value that can be set and get. If multiple users set the value at the same time, you pick one of them arbitrarily, or perhaps average them together.

Example uses for Registers:

Registers are very useful and suffice for many tasks (e.g., Figma and Hex use them almost exclusively).

The only operation on a Register is set(x), which sets the value to x (in the absence of concurrent operations). We can’t perform these operations literally, since if two users receive concurrent set operations in different orders, they’ll end up with different values.

However, we can add the value x to a Unique Set, following Principle 1. The state is now a set of values instead of a single value, but we’ll address that soon. We can also delete old values each time set(x) is called, overwriting them.

Thus the implementation of set(x) becomes:

The result is that at any time, the Register’s state is the set of all the most recent concurrently-set values.

Loops of the form “for each element of a collection, do something” are common in programming. We just saw a way to extend them to CRDTs: “for each element of a Unique Set, do some CRDT operation”. I call this a causal for-each operation because it only affects elements that are prior to the for-each operation in the causal order. It’s useful enough that we make it our next principle of CRDT design:

Principle 3a. For operations that do something “for each” element of a collection, one option is to use a causal for-each operation on a Unique Set (or List CRDT).

(Later we will expand on this with Principle 3b, which also concerns for-each operations.)

Returning to Registers, we still need to handle the fact that our state is a set of values, instead of a specific value.

One option is to accept this as the state, and present all conflicting values to the user. That gives the Multi-Value Register (MVR).

Another option is to pick a value arbitrarily but deterministically. E.g., the Last-Writer Wins (LWW) Register tags each value with the wall-clock time when it is set, then picks the value with the latest timestamp.

Grid of pixels, some conflicting (outlined in red). One conflicting pixel has been clicked on, revealing the conflicting choices.

In Pixelpusher, a collaborative pixel art editor, each pixel shows one color by default (LWW Register), but you can click to pop out all conflicting colors (MVR). Image credit: Peter van Hardenberg (original).

In general, you can define the value getter to be an arbitrary deterministic function of the set of values.

Examples:

Composing CRDTs

We now have enough basic CRDTs to start making more complicated data structures through composition. I’ll describe three techniques: CRDT Objects, CRDT-Valued Maps, and collections of CRDTs.

CRDT Objects

The simplest composition technique is to use multiple CRDTs side-by-side. By making them instance fields in a class, you obtain a CRDT Object, which is itself a CRDT (trivially correct). The power of CRDT Objects comes from using standard OOP techniques, e.g., implementation hiding.

Examples:

To implement a CRDT Object, each time an instance field requests to broadcast a message, the CRDT Object broadcasts that message tagged with the field’s name. Receivers then deliver the message to their own instance field with the same name.

CRDT-Valued Map

A CRDT-Valued Map is like a CRDT Object but with potentially infinite instance fields, one for each allowed map key. Every key/value pair is implicitly always present in the map, but values are only explicitly constructed in memory as needed, using a predefined factory method (like Apache Commons’ LazyMap).

Examples:

A CRDT-Valued Map is implemented like a CRDT Object: each message broadcast by a value CRDT is tagged with its serialized key. Internally, the map stores only the explicitly-constructed key-value pairs; each value is constructed using the factory method the first time it is accessed by the local user or receives a message. However, this is not visible externally—from the outside, the other values still appear present, just in their initial states. (If you want an explicit set of “present” keys, you can track them using an Add-Wins Set.)


Collections of CRDTs

Our above definition of a Unique Set implicitly assumed that the data values x were immutable and serializable (capable of being sent over the network). However, we can also make a Unique Set of CRDTs, whose values are dynamically-created CRDTs.

To add a new value CRDT, a user sends a unique new tag and any arguments needed to construct the value. Each recipient passes those arguments to a predefined factory method, then stores the returned CRDT in their copy of the set. When a value CRDT is deleted, it is forgotten and can no longer be used.

Note that unlike in a CRDT-Valued Map, values are explicitly created (with dynamic constructor arguments) and deleted—the set effectively provides collaborative new and free operations.

We can likewise make a List of CRDTs.

Examples:

Using Composition

You can use the above composition techniques and basic CRDTs to design CRDTs for many collaborative apps. Choosing the exact structure, and how operations and user-visible state map onto that structure, is the main challenge.

A good starting point is to design an ordinary (non-CRDT) data model, using ordinary objects, collections, etc., then convert it to a CRDT version. So variables become Registers, objects become CRDT Objects, lists become List CRDTs, sets become Unique Sets or Add-Wins Sets, etc. You can then tweak the design as needed to accommodate extra operations or fix weird concurrent behaviors.

To accommodate as many operations as possible while preserving user intention, I recommend:

Principle 4. Independent operations (in the user’s mind) should act on independent state.

Examples:

New: Concurrent+Causal For-Each Operations

There’s one more trick I want to show you. Sometimes, when performing a for-each operation on a Unique Set or List CRDT (Principle 3a), you don’t just want to affect existing (causally prior) elements. You also want to affect elements that are added/inserted concurrently.

For example:

I call such an operation a concurrent+causal for-each operation. To accomodate the above examples, I propose the following addendum to Principle 3a:

Principle 3b. For operations that do something “for each” element of a collection, another option is to use a concurrent+causal for-each operation on a Unique Set (or List CRDT).

To implement this, the initiating user first does a causal (normal) for-each operation. They then send a message describing how to perform the operation on concurrently added elements. The receivers apply the operation to any concurrently added elements they’ve received already (and haven’t yet deleted), then store the message in a log. Later, each time they receive a new element, they check if it’s concurrent to the stored message; if so, they apply the operation.

Aside. It would be more general to split Principle 3 into “causal for-each” and “concurrent for-each” operations, and indeed, this is how the previous paragraph describes it. However, I haven’t yet found a good use case for a concurrent for-each operation that isn’t part of a concurrent+causal for-each.


Concurrent+causal for-each operations are novel as far as I’m aware. They are based on a paper I, Heather Miller, and Christopher Meiklejohn wrote last year, about a composition technique we call the semidirect product, which can implement them (albeit in a confusing way). Unfortunately, the paper doesn’t make clear what the semidirect product is doing intuitively, since we didn’t understand this ourselves! My current opinion is that concurrent+causal for-each operations are what it’s really trying to do; the semidirect product itself is (a special case of) an optimized implementation, improving memory usage at the cost of simplicity.

Summary: CRDT Design Techniques

That’s it for our CRDT design techniques. Before continuing to the spreadsheet case study, here is a summary cheat sheet.

Case Study: A Collaborative Spreadsheet

Now let’s get practical: we’re going to design a CRDT for a collaborative spreadsheet editor (think Google Sheets).

As practice, try sketching a design yourself before reading any further. The rest of this section describes how I would do it, but don’t worry if you come up with something different—there’s no one right answer! The point of this blog post is to give you the confidence to design and tweak CRDTs like this yourself, not to dictate “the one true spreadsheet CRDT™”.

Design Walkthrough

To start off, consider an individual cell. Fundamentally, it consists of a text string. We could make this a Text (List) CRDT, but usually, you don’t edit individual cells collaboratively; instead, you type the new value of the cell, hit enter, and then its value shows up for everyone else. This suggests instead using a Register, e.g., an LWW Register.

Besides the text content, a cell can have properties like its font size, whether word wrap is enabled, etc. Since changing these properties are all independent operations, following Principle 4, they should have independent state. This suggests using a CRDT Object to represent the cell, with a different CRDT instance field for each property. In pseudocode (using extends CRDTObject to indicate CRDT Objects):

class Cell extends CRDTObject {
  content: LWWRegister<string>;
  fontSize: LWWRegister<number>;
  wordWrap: EnableWinsFlag;
  // ...
}

The spreadsheet itself is a grid of cells. Each cell is indexed by its location (row, column), suggesting a map from locations to cells. (A 2D list could work too, but then we’d have to put rows and columns on an unequal footing, which might cause trouble later.) Thus let’s use a Cell-CRDT-Valued Map.

What about the map keys? It’s tempting to use conventional row-column indicators like “A1”, “B3”, etc. However, then we can’t easily insert or delete rows/columns, since doing so renames other cells’ indicators. (We could try making a “rename” operation, but that violates Principle 2, since it does not match the user’s original intention: inserting/deleting a different row/column.)

Instead, let’s identify cell locations using pairs (row, column), where “row” means “the line of cells horizontally adjacent to this cell”, independent of that row’s literal location (1, 2, etc.), and likewise for “column”. That is, we create an opaque Row object to represent each row, and likewise for columns, then use pairs (Row, Column) for our map keys.

The word “create” suggests using Unique Sets (Principle 1), although since the rows and columns are ordered, we actually want List CRDTs. Hence our app state looks like:

rows: ListCRDT<Row>;
columns: ListCRDT<Column>;
cells: CRDTValuedMap<[row: Row, column: Column], Cell>;

Now you can insert or delete rows and columns by calling the appropriate operations on columns and rows, without affecting the cells map at all. (Due to the lazy nature of the map, we don’t have to explicitly create cells to fill a new row or column; they implicitly already exist.)

Speaking of rows and columns, there’s more we can do here. For example, rows have editable properties like their height, whether they are visible, etc. These properties are independent, so they should have independent states (Principle 4). This suggests making Row into a CRDT Object:

class Row extends CRDTObject {
  height: LWWRegister<number>;
  isVisible: EnableWinsFlag;
  // ...
}

Also, we want to be able to move rows and columns around. We already described how to do this using a List-with-Move CRDT:

class MovableListEntry<C> extends CRDTObject {
  value: C;
  positionReg: LWWRegister<UniqueImmutablePosition>;
}

class MovableListOfCRDTs<C> extends CRDTObject {
  state: UniqueSetOfCRDTs<MovableListEntry<C>>;
}


rows: MovableListOfCRDTs<Row>;
columns: MovableListOfCRDTs<Column>;

Next, we can also perform operations on every cell in a row, like changing the font size of every cell. For each such operation, we have three options:

  1. Use a causal for-each operation (Principle 3a). This will affect all current cells in the row, but not any cells that are created concurrently (when a new column is inserted). E.g., a “clear” operation that sets every cell’s value to "".
  2. Use a concurrent+causal for-each operation (Principle 3b). This will affect all current cells in the row and any created concurrently. E.g., changing the font size of a whole row.
  3. Use an independent state that affects the row itself, not the cells (Principle 4). E.g., our usage of Row.height for the height of a row.

Finished Design

In summary, the state of our spreadsheet is as follows.

// ---- CRDT Objects ----
class Row extends CRDTObject {
  height: LWWRegister<number>;
  isVisible: EnableWinsFlag;
  // ...
}

class Column extends CRDTObject {
  width: LWWRegister<number>;
  isVisible: EnableWinsFlag;
  // ...
}

class Cell extends CRDTObject {
  content: LWWRegister<string>;
  fontSize: LWWRegister<number>;
  wordWrap: EnableWinsFlag;
  // ...
}

class MovableListEntry<C> extends CRDTObject {
  value: C;
  positionReg: LWWRegister<UniqueImmutablePosition>;
}

class MovableListOfCRDTs<C> extends CRDTObject {
  state: UniqueSetOfCRDTs<MovableListEntry<C>>;
}

// ---- App state ----
rows: MovableListOfCRDTs<Row>;
columns: MovableListOfCRDTs<Column>;
cells: CRDTValuedMap<[row: Row, column: Column], Cell>;

Note that I never explicitly mentioned CRDT correctness—the claim that all users see the same document state after receiving the same messages. Because we assembled the design from existing CRDTs using composition techniques that preserve CRDT correctness, it is trivially correct. Plus, it should be straightforward to reason out what would happen in various concurrency scenarios.

As exercises, here are some further tweaks you can make to this design, phrased as user requests:

  1. “I’d like to have multiple sheets in the same document, accessible by tabs at the bottom of the screen, like in Excel.” Hint (highlight to reveal): Use a List of CRDTs.
  2. “I’ve noticed that if I change the font size of a cell, while at the same time someone else changes the font size for the whole row, sometimes their change overwrites mine. I’d rather keep my change, since it’s more specific.” Hint: Use a Register with a custom getter.
  3. “I want to reference other cells in formulas, e.g., = A2 + B3. Later, if B3 moves to C3, its references should update too.” Hint: Store the reference as something immutable.

Conclusion

I hope you’ve gained an understanding of how CRDTs work, plus perhaps a desire to apply them in your own apps. We covered a lot:

For more info, crdt.tech collects most CRDT resources in one place. For traditional CRDTs, the classic reference is Shapiro et al. 2011, while Preguiça 2018 gives a more modern overview.

I’ve also put many of these ideas into practice in a library, Collabs. You can learn more about Collabs, and see how open-source collaborative apps might work in practice, in my Local-First Web talk: Video, Slides, Live demo.

This blog post’s approach to CRDT design - using simple CRDTs plus composition techniques - draws inspiration from a number of sources. Most similar is the way Figma and Hex describe their collaboration platforms; they likewise support complex apps by composing simple, easy-to-reason-about pieces. Relative to those platforms, I incorporate more academic CRDT designs, enabling more flexible behavior and server-free operation.

The specific CRDTs I describe are based on Shapiro et al. 2011 unless noted otherwise. Note that they abbreviate “Unique Set” to “U-Set”. For composition techniques, a concept analogous to CRDT Objects appears in BloomL; CRDT-Valued Maps appear in Riak and BloomL; and the Collections of CRDTs are inspired by how Yjs’s Y.Array and Y.Map handle nested CRDTs.

Similar to how I build everything on top of a Unique Set CRDT, Mergeable Replicated Data Types are all built on top of a (non-unique) set with a 3-way merge function, but in a quite different way.

Other systems that allow arbitrary nesting of CRDTs include Riak, Automerge, Yjs, and OWebSync.

Acknowledgments

I thank Heather Miller, Ria Pradeep, and Benito Geordie for numerous CRDT design discussions that led to these ideas. Jonathan Aldrich, Justine Sherry, and Pratik Fegade reviewed a version of this post that appears on the CMU CSD PhD Blog. I am funded by an NDSEG Fellowship sponsored by the US Office of Naval Research.

Appendix: What’s Missing?

The CRDT design techniques I describe above are not sufficient to reproduce all published CRDT designs - or more generally, all possible Strong Eventual Consistency data structures. This is deliberate: I want to restrict to (what I consider) reasonable semantics and simple implementations.

In this section, I briefly discuss some classes of CRDTs that aren’t covered by the above design techniques.

Optimized Implementations

Given a CRDT designed using the above techniques, you can often find an alternative implementation that has the same semantics (user-visible behavior) but is more efficient.

For example:

My advice is to start with an implementation using the techniques in this blog post. That way, you can pin down the semantics and get a proof-of-concept running quickly. Later, if needed, you can make an alternate, optimized implementation that has the exact same user-visible behavior as the original (enforced by mathematical proofs, unit tests, or both).

Doing things in this order - above techniques, then optimize - should help you avoid some of the difficulties of traditional, from-scratch CRDT design. It also ensures that your resulting CRDT is both correct and reasonable. In other words: beware premature optimization!

3 out of 4 Peritext authors mention that it was difficult to get working: here, here, and here.


One way to optimize is with a complete rewrite at the CRDT level. For example, relative to the rich text CRDT that we sketched above (enhanced with concurrent+causal for-each operations), Peritext looks like a complete rewrite. (In reality, Peritext came first.)

Another option is to “compress” the CRDT’s state/messages in some way that is easy to map back to the original CRDT. That is, in your mind (and in the code comments), you are still using the CRDT derived from this blog post, but the actual code operates on some optimized representation of the same state/messages.

For example, in the rich text CRDT sketched above, if storing separate formatting registers for each character uses too much memory, you could compress the state by deduplicating the identical formatting entries that result when a user formats a range of text. Then the next time you receive an operation, you decompress the state, apply that operation, and recompress. Likewise, if formatting a range of characters individually generates too much network traffic (since there is one CRDT message per character), you could instead send a single message that describes the whole formatting operation, then have recipients decompress it to yield the original messages.

Optimized Semantics

Some existing CRDTs deliberately choose behavior that may look odd to users, but has efficiency benefits. The techniques in this blog post don’t always allow you to construct those CRDTs.

The example that comes to my mind concerns what to do when one user deletes a CRDT from a CRDT collection, while concurrently, another user makes changes to that CRDT. E.g., one user deletes a presentation slide while someone else is editing the slide. There are a few possible behaviors:

I am okay with not supporting odd semantics because user experience seems like a first priority. If your desired semantics results in poor performance (e.g. “archiving” semantics leading to unbounded memory usage), you can work around it once it becomes a bottleneck, e.g., by persisting some state to disk.

Hard Semantics

Some CRDTs seem useful and not prematurely optimized, but I don’t know how to implement them using the techniques in this blog post. Two examples:

Aside. There is a sense in which the Unique Set CRDT (hence this blog post) is “CRDT-complete”, i.e., it can be used to implement any CRDT semantics: you use a Unique Set to store the complete operation history together with causal ordering info, then compute the state as a function of this history, like in pure op-based CRDTs. However, this violates the spirit of the blog post, which is to give you guidance on how to design your CRDT.

Beyond CRDTs

CRDTs, and more broadly Strong Eventual Consistency, are not everything. Some systems, including some collaborative apps, really need Strong Consistency: the guarantee that events happen in a serial order, agreed upon by everyone. E.g., monetary transactions. So you may need to mix CRDTs with strongly consistent data structures; there are a number of papers about such “Mixed Consistency” systems, e.g., RedBlue consistency.

Home • Matthew Weidner • PhD student at CMU CSD • mweidner037 [at] gmail.com • @MatthewWeidner3 • LinkedIn • GitHub