Fugue: A Basic List CRDT

Matthew Weidner | Oct 21st, 2022
Home | RSS Feed
Keywords: collaborative text editing, CRDTs, Lists, Fugue, Plain Tree

Update: This post was previously titled “Plain Tree: A Basic List CRDT”. Since posting, I and Martin Kleppmann wrote a paper about this list CRDT and renamed it Fugue.

The main ideas in this post are described in slides here.

Collaborative text editing was the original motivation for Conflict-free Replicated Data Types (CRDTs) (WOOT 2005), and it is still a popular use case. It is also the most difficult CRDT application: the underlying List CRDTs have complicated algorithms and implementations, and there are a lot of them spread throughout academic papers and software libraries. This makes them intimidating to study.

In this post, I describe Fugue, a basic List CRDT that I find fairly easy to understand, plus some simple implementations. My goal is that you will also understand it, filling in a gap from my previous post. Despite its simplicity, the CRDT described here is my preferred List CRDT. In particular, Collabs uses it for all list implementations.

You don’t need to have read the previous post, Designing Data Structures for Collaborative Apps, but its introduction may be useful if you are new to CRDTs and collaborative editing.

What We Need: A “Uniquely Dense Total Order”

To start, let’s think about making a collaborative plain text editor, like this Collabs demo. The editor’s state is a text string, replicated on each user’s device, such that any user can insert (type) or delete characters from the string.

In usual CRDT style, we mandate that all users see their own changes immediately, but also reflect other users’ changes once they receive them, possibly after an unbounded network delay. The end result must be consistent across all users (CRDT correctness/strong eventual consistency) and should also be “reasonable”, e.g., edits to two different parts of the text each show up as expected.

We can generalize this problem to collaborating on arbitrary lists of immutable values. Collaborating text editing is a special case: a list of characters. A List CRDT is a CRDT for such lists, with insert and delete operations. Formally, the operations on a List CRDT are:

• insert(i, x): Inserts a new element with value x at index i, between the existing elements at indices i and i+1. All later elements (index >= i+1) are shifted one to the right.
• delete(i): Deletes the element at index i. All later elements (index >= i+1) are shifted one the left.

Handling concurrent operations—while ensuring that the results are consistent for all users and also reasonable—is tricky because concurrent operations mess up each others’ indices.

Alice typed " the" at index 17, but concurrently, Bob typed " gray" in front of her. From Bob's perspective, Alice's insert should happen at index 22.

To handle this, most List CRDTs abandon indices internally. Instead, they assign each list element a unique immutable position at the time of insertion, which abstractly describes how to sort elements relative to each other. The user-visible state of the List CRDT is just the elements sorted by their positions. insert and delete internally operate on positions, only using their index argument i to look up the current positions at/near that index.

If two users insert elements concurrently, then those elements are sorted based on their positions. Since all users see the same positions (and the same sort order on positions), they all sort these concurrent elements identically, ensuring CRDT correctness. Deleting one element doesn’t affect the positions of any other elements, so it is easy to ensure correctness for delete operations as well (see my previous post for details).

So, to make our List CRDT (hence our collaborative plain text editor), all we need is a way to sort and create these unique immutable positions. In other words, we need an implementation of the following TypeScript interface (also on GitHub):

/**
 * Helper interface for sorting and creating unique immutable positions,
 * suitable for use in a List CRDT.
 *
 * @type P The type of positions. Treated as immutable.
 */
export interface UniquelyDenseTotalOrder<P> {
  /**
   * Usual compare function for sorts: returns negative if a < b in
   * their sort order, positive if a > b.
   */
  compare(a: P, b: P): number;

  /**
   * Returns a globally unique new position c such that a < c < b.
   *
   * "Globally unique" means that the created position must be distinct
   * from all other created positions, including ones created concurrently
   * by other users.
   *
   * When a is undefined, it is treated as the start of the list, i.e.,
   * this returns c such that c < b. Likewise, undefined b is treated
   * as the end of the list.
   */
  createBetween(a: P | undefined, b: P | undefined): P;
}

Mathematically, this interface says that positions must be drawn from a total order, with two extra requirements:

• It is dense: between any two elements a < b, there is a c such that a < c < b.
• Furthermore, it is uniquely dense: users can request a new globally unique such c between any a < b. (Unlike “dense total order”, this is not a standard math term.)

A few notes about the UniquelyDenseTotalOrder interface:

• An implementation may choose to have state that it uses in compare and createBetween. For example, an optimized implementation will often store all the positions it has seen in a sorted data structure, then use that to answer compare calls quickly.
• An implementation may choose to behave like a CRDT itself, e.g,. by broadcasting messages to replicas of the UniquelyDenseTotalOrder on different devices (op-based CRDT) and/or by implementing a merge function (state-based CRDT). For example, an implementation might broadcast newly-created positions to other users in createBetween, together with metadata needed to compare them to existing positions.

You may be familiar with fractional indexing, which uses a dense total order, and wonder how UniquelyDenseTotalOrder differs. The answer is our added “globally unique” requirement: if two users call createBetween(a, b) concurrently for the same a and b, then we require both users to get different results. That way, it’s later possible to createBetween those two results.

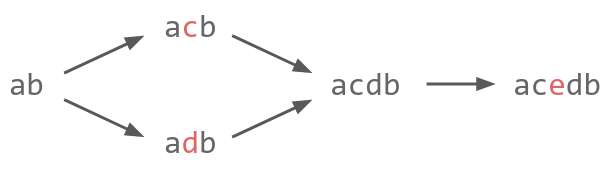
Starting from text "ab", two users concurrently type 'c' and 'd' at the same place. After syncing, the order of 'c' and 'd' is arbitrary but must be consistent across all users; suppose 'c' is first, so the text is now "acdb". Later, a user might try to type 'e' in between 'c' and 'd'. This doesn't work with fractional indexing because 'c' and 'd' have the same position - there are no positions "between" them. But it does work in a UniquelyDenseTotalOrder-based List CRDT, due to our global uniqueness requirement.

A Basic Uniquely Dense Total Order

It remains to implement UniquelyDenseTotalOrder. That’s what most List CRDT papers do, although they usually wrap it in the UniquelyDenseTotalOrder-to-List-CRDT conversion.

The rest of this post introduces a basic UniquelyDenseTotalOrder that I especially like. Update: You can find more info in the paper “The Art of the Fugue: Minimizing Interleaving in Collaborative Text Editing” by myself and Martin Kleppmann.

I’ll focus on describing its semantics—how its created positions compare to each other, independent of their literal representation—and two simple, unoptimized implementations. In future posts, I hope to go into detail about properties, comparisons to other List CRDTs, and optimized implementations.

Intro: String Implementation

Strings make good positions because they are already ordered, immutable, and can be made arbitrarily long. You can even sort them in CRDT-unaware contexts, e.g., sorting a List CRDT’s elements in a database using ORDER BY positions.

To make a UniquelyDenseTotalOrder<string>, we really just need to implement createBetween: given strings a and b with a < b in the lexicographic order, return a unique new string in between.

Here’s a simple way to do this:

• For convenience, we require that all positions end in 'R'.
• If a is not a prefix of b, append a globally unique new string to a (see next paragraph) and return that plus 'R'. This will be greater than a because it’s longer, and less than b for the same reason that a < b.
• If a is a prefix of b (necessarily strictly shorter):
  1. Replace the 'R' at the end of b with an 'L'.
  2. Append a globally unique new string to that (see next paragraph) and return it plus 'R'. This will be less than b because 'L' < 'R', and greater than a because a is still a strictly-shorter prefix.

How do we get a globally unique new string? One strategy is to make it random and sufficiently long, e.g., a UUID. However, UUIDs are rather long, making it inefficient to send positions over the network. Instead, we use a causal dot: a pair (replicaID, counter), where replicaID is a reasonably short ID for the local replica (device)—say 10 random characters—and counter is a local counter incremented for each causal dot.

In code (complete code here):

class StringFugue implements UniquelyDenseTotalOrder<string> {
  /**
   * Local replica ID, set in constructor.
   * All replicaIDs have the same length.
   */
  readonly replicaID: string;
  // Local counter.
  private counter = 0;

  createBetween(a: string | undefined, b: string | undefined): string {
    // A globally unique new string, in the form of a causal dot.
    const uniqueStr = `${this.replicaID}${this.counter++}`;
    
    if (a !== undefined && b !== undefined) {
      if (!b.startsWith(a)) {
        // a is not a prefix of b.
        return a + uniqueStr + 'R';
      } else {
        // a is a strict prefix of b.
        const bWithL = b.slice(0, -1) + 'L';
        return bWithL + uniqueStr + 'R';
      }
    } else {
      // Edge cases...
    }
  }
  
  // compare...
}

Or, a code golf version (note: slightly different positions):

class GolfStringFugue implements UniquelyDenseTotalOrder<string> {
  readonly id: string;
  private c = 0;

  createBetween(a = "R", b = "Z"): string {
    return (
      // "One line" List CRDT :)
      (b.startsWith(a) ? b.slice(0, -1) + "L" : a) + `${this.id}${this.c++}R`
    );
  }

  // ...
}

I wouldn’t recommend using these exact implementations due to their large position sizes, but they could be useful in a pinch.

Semantics

The string implementation above works, but we’d like to understand it better.

I claim that mathematically, we can model our uniquely dense total order as a rooted binary-ish tree:

• Each node in the tree, except for the root, has a parent and a side (left or right child). Multiple nodes can have the same parent and side, which is why it is “binary-ish” instead of binary.
• Each node is labelled by a causal dot.
• The sort order on nodes is given by the tree walk (in-order traversal): first traverse a node’s left children, then visit the node, then traverse its right children. Ties between children on the same side are broken using the causal dots.
• Positions are given by nodes in the tree.

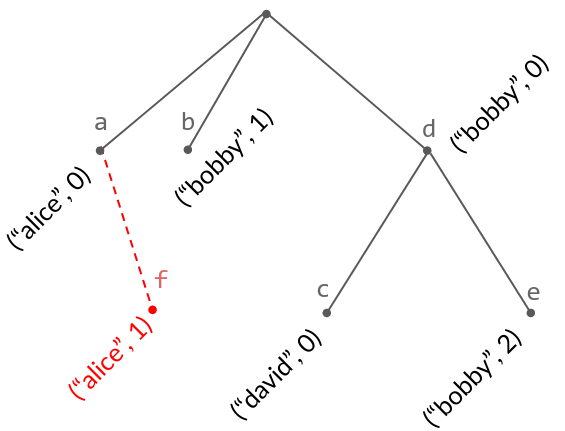
Example of a tree with corresponding text "abcde". Observe that the root has two left children, sorted by their causal dots; this can happen due to concurrent insertions.

The same tree with a new node ("alice", 2), inserted as a right child of ("alice", 0). Its text is now "afbcde". Note that this insertion corresponds to the hard case above (though with different text).

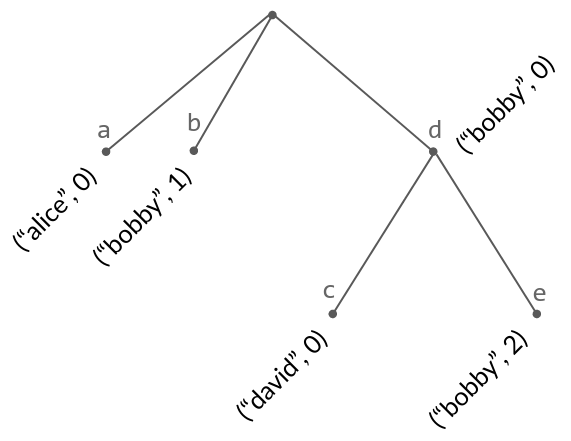
In our string implementation, each string position describes a path in this tree, starting at the root: it alternates between listing the next node’s ID, and an 'L' or 'R' indicating whether the following node is a left or right child.

You can check that the lexicographic order on strings then matches our sort order on tree nodes: the 'L's and 'R's ensure that a string position is sorted in between its left and right descendants in the tree (since "L..." < "R" < "R..."), and the lexicographic order on IDs matches the tree’s tie-breaking rule.

Finally, createBetween(a, b) works as follows:

• If a is not an ancestor of b, create a new node as a right child of a, labeled by a new causal dot, and return that. (Example above.)
• If a is an ancestor of b, create a new node as a left child of b, labeled by a new causal dot, and return that. (Example immediately below.)

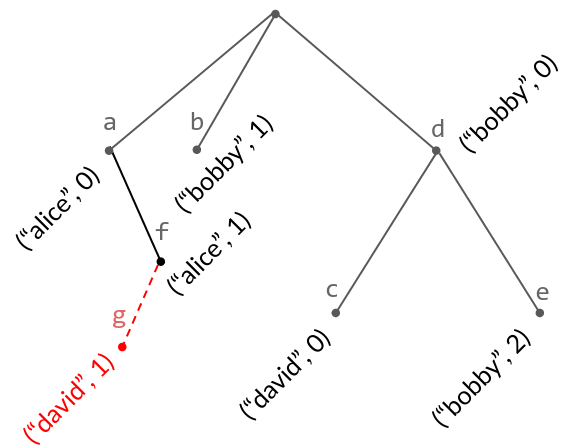
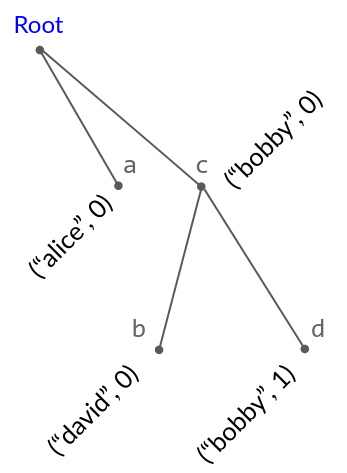
The tree from above with another new node, ("david", 1). This time, it is a *left* child of ("alice", 1), since its left neighbor ("alice", 0) already has a right descendant. The text is now "agfbcde".

Tree Implementation

We can implement our tree-based description literally. That is, we can program a UniquelyDenseTotalOrder using an explicit tree data stucture, instead of using the string implementation’s implicit tree.

The last section’s description is not quite an actual algorithm: it describes Fugue in terms of a single, global view of the tree, but in reality, each user has their own local copy of the tree. These local copies may be out of sync: there can be an arbitrary delay between when one user calls createBetween and when other users hear about the created position.

The real algorithm is:

• A position is represented as a causal dot.
• Each user has, as local state, a binary-ish tree of the above form.
• In createBetween, the user creates a new node in its local tree as described above. It broadcasts the node’s causal dot, parent causal dot, and side (left or right child) to all other users; upon receiving this message, the other users add that node to their own local tree. createBetween returns the node’s label (causal dot) as the created position.
• In compare(a, b), the user finds nodes with labels a and b in its local tree. It then compares those nodes by their sort order in the tree walk.

The implicit global tree we described in Semantics corresponds to the union of all users’ local trees. Describing things in terms of this global tree makes sense because (1) local trees and the global tree both only grow over time—they don’t remove or modify existing nodes—and (2) a user only receives calls to compare or createBetween on nodes that it has in its local tree, and it returns the same answer as the global tree.

Here we assume message delivery in causal order, to ensure that when a user receives a node broadcast by createBetween, it has already received the parent node.

Code for this algorithm is here.

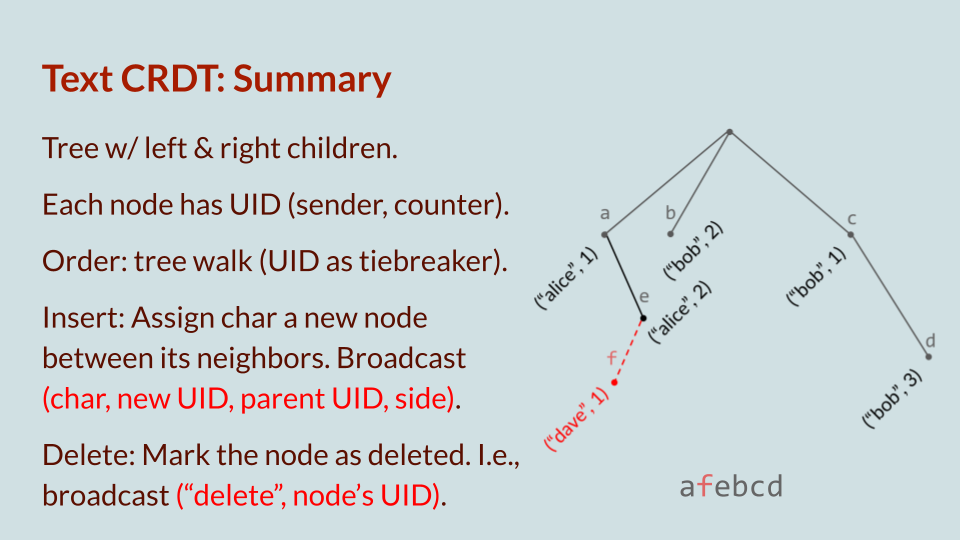
We can summarize the resulting List CRDT with a single slide:

Comparing the Implementations

Relative to our first string implementation, this tree implementation has much better network efficiency: its positions - which the corresponding List CRDT will broadcast to other clients over the network - have small constant size (~15 bytes), and likewise for the messages broadcast by createBetween (~30 bytes with optimized encoding). This contrasts with the string positions, which can become arbitrarily long.

However, the tree implementation has worse memory usage: each user needs to store a copy of the entire tree, including positions that are no longer used by the outer List CRDT (tombstones). Also, it is hard to use the tree implementation’s positions in CRDT-unaware contexts, since they can’t be compared directly like strings.

See also: the LSEQ paper’s discussion of tombstones vs variable-size identifiers for List CRDTs.

In practice, you’ll want to use a more optimized implementation than either of the two described here. I hope to discuss these later, but for now, note that Collabs’s list data structures (e.g. CText) all use an optimized version of the tree implementation.

Aside. I think of both implementations as variations on “the same” Fugue List CRDT. However, the CRDT literature sometimes assigns different names to List CRDTs that are substantially similar except for (say) different optimizations, e.g., LSEQ vs. Logoot. At the other extreme, it is sometimes to possible to find two very different algorithms with the same user-visible behavior: given a (distributed) trace of compare and createBetween (or insert and delete) operations, they assign positions with the same sort orders. The example I have in mind is Seph Gentle’s description of a YATA-style algorithm implementing RGA’s behavior (section “Improving the data structure”). An old version of the Fugue paper described a similar algorithm equivalent to Fugue (“List-Fugue”); it’s omitted from the current version for length reasons, but we (myself, Seph, and Martin) hope to formalize it in a future tech report.

Conclusion

I hope the above description of the Fugue List CRDT made sense and was not too intimidating. If you’ve also read Designing Data Structures for Collaborative Apps, you now know what I consider the fundamentals of CRDTs-for-collaboration.

As I mentioned, Fugue is my preferred List CRDT. In future posts, I hope to detail why this is, and also put it in context within the List CRDT literature. So look forward to posts on:

• Fugue’s “non-interleaving” guarantees.
• Other List CRDTs: Logoot, Treedoc, RGA, LSEQ, YATA, and how they relate to Fugue.
• Efficient implementations.

Update: You can find info about most of these topics (non-interleaving guarantees, relation to RGA and YATA/Yjs, and efficient implementations) in the Fugue paper.

In the meantime, feel free to ask me about these directly.

Working TypeScript code for the above snippets is on GitHub.

Home • Matthew Weidner • PhD student at CMU CSD • mweidner037 [at] gmail.com • @MatthewWeidner3 • LinkedIn • GitHub